アロワナ

アロワナ
このページでは”泳ぎ”のアルゴリズムについて説明します。
このロボットを計画している段階では、主に”アロワナ”の泳ぎを観察し
ました。(非常にゆっくりと絶えず動いているので観察しやすいです。
また、どのペットショップで、もたいてい見やすく展示して売られています。)
観察の結果、体(尾部)に沿って、進行にしたがい振幅の増える
”表面波”(水面に出来るような波)を進ませる方針でプログラムを
書くことにしました。波形は3角関数の組み合わせで作りました。
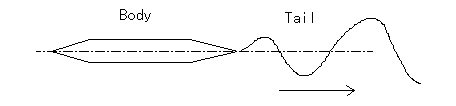
波状運動の概念図
下に一定スピードで直進する時の制御波形を示します。系列1,2,3がそれぞれ 体の前から後ろに向かってサーボ0,1,2用のデータになります。縦軸が サーボに出力するデータ(8ビットなので0〜255です)、横軸が時間です。
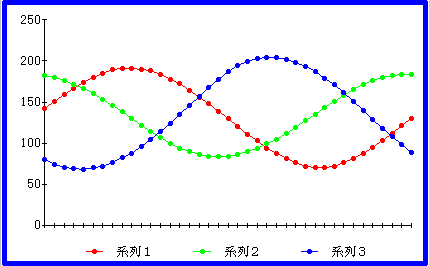
直進用制御波形
結果的には、それらしい形で動かすことが出来ました。震動翼推進形式の 船に関する、客観的な推進効率の評価方法を知らないので、なんともいえませんが、 見た目は同じサイズのコイが、同じペースで体を動かしているときの7割くらいで 前に進んでいるように見えます。
本機では、波状運動の周期、振幅、波の形を変えることによって
移動速度を制御しています。
一定の転送レートで信号発生ボードへサーボ出力データを
書き込んでいるので、同じ波形の再生スピードを変える場合は、
波形の時間分割の密度を変えます。(同じ波形を少ないデータ数で
構成すれば早く動き、多いデータ数で構成すればゆっくりと動きます。)
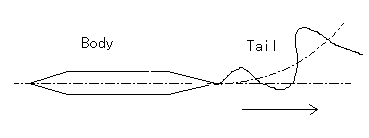
旋回時の波状運動
遷移波形:停止状態から直進状態に移る場合や、直進から旋回に 移る場合など、ある制御波形から別の波系に移る途中で使う制御波形です。 二つの波形の間を直線補間?して作ってあります。