歩行アルゴリズムのページ

概要

このページでは歩行アルゴリズムについて説明します。 なにをどう書くかについては、非常に悩むところです。２足歩行の説明そのものについては 本や論文がたくさんあるので、２Ｌ１で試したこと、その結果、考察（というよりは感想） 、考えた力学モデルを、しばらくは徒然なるままに書きます。あるていど 量がまとまってきたら、編集しようと思っています。

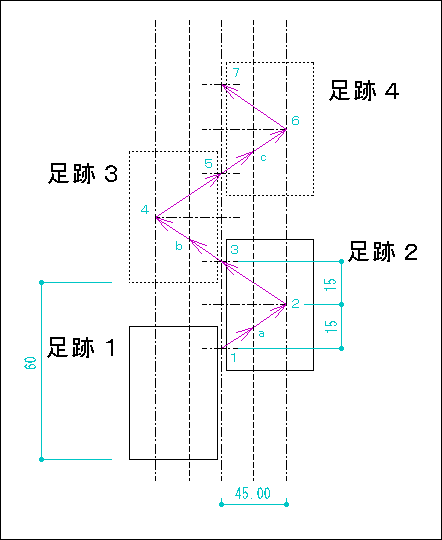
足の運び方（直進歩行のパターン） １．標記の説明 足跡１〜４：足跡です。 紫の線：下図で説明している「仮重心」の移動軌跡を地面へ投影した線です。 寸法：実際に２Ｌ１ｖ６で使用した歩行パターンのパラメーターです。 ２．歩き方の説明 区間「１」−＞「２」 左図は足をそろえた状態から「はじめの一歩」を経て連続的に歩いている状態を 示しています。図から分かるように「仮重心」はジグザグに移動してゆきます。 「１」−＞「２」は右足に重心を移してゆく過程を表しています。仮重心は「１」で 加速をはじめ、「１」と「２」の中間点で最高速度に達し、「２」で停止します。 途中仮重心が「ａ」まで来たときに左足を前に出し始めます。 「ａ」の位置は、実際に歩かせながら１から２の中間点付近に決めます。 左足は「仮重心」が「ａ」から「２」へ移動する時間で「足跡１」から 「足跡３」へ移動します。「足跡３」に到着した時点で左足は数ミリ 浮かせておきます。 区間「２」−＞「３」 「仮重心」を左右の足の中心まで戻します。 この間に左足を地面の高さまで下ろします。 「仮重心」の移動速度はやはり中間点で最高となります。 区間「３」−＞「４」 「１」−＞「２」と同じです。 区間「４」−＞「５」 「２」−＞「３」と同じです。 以上「１」−＞「５」で１サイクルを構成します。ここで１，３，５点では ロボットの重心が両足の中間にあり、停止しています。この状態を「軌道切り替え 点」（直進から旋回等）と「モーターに負担の少ない停止点」として使用しました。 ３．軌跡の分割数 ＲＣサーボの目標位置の更新レートは毎秒２５回で、「１」−＞「２」等 各直線区間の分割数は１９〜２２です。内蔵する電池の重量により加減しています。 （重心が変わると揺れの周期が変わるためです。） 周期が変わったときにはジャイロのゲインも変えた方が良いのですが、しませんでした。

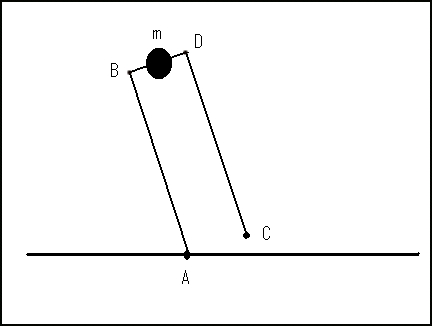
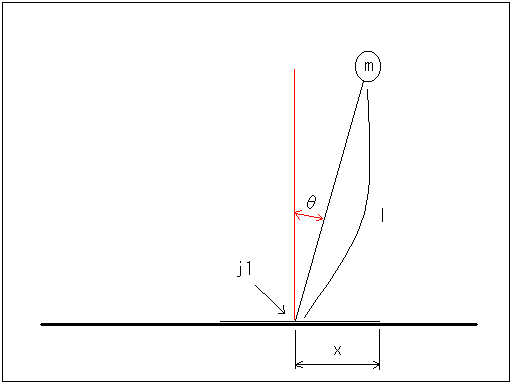
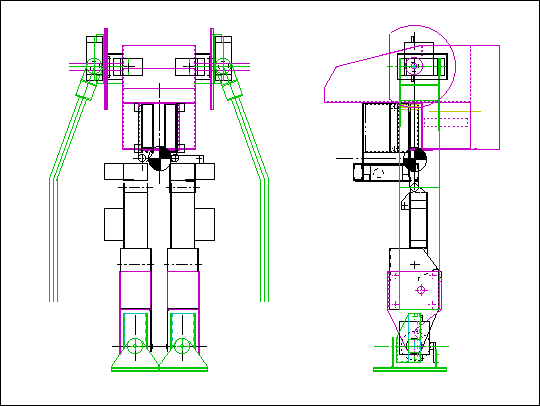
計算の基準点（仮重心） 左図の「重心マーク？」の場所を仮に重心位置と決めて、この仮重心の移動軌跡と、遊脚 （体を支えていない方の足）の軌跡を制御波形生成プログラムへの入力としています。 また、この場所は逆運動学計算を行うとき、各関節の位置を定義する「原点」としても 使っています。

自動車等の「アクティブサスペンション」の考え方を取り入れています。 ごく一般的な自動車のサスペンションにはバネとオイルダンパーが付いて 受動的に動くだけですが、私が指す「アクティブサスペンション」とは、 このバネ・ダンパー系の特性をアクチュエーターの制御でシミュレート する事により、衝撃を吸収すると言うものです。

２Ｌ１ｖ５の動画を注意深く見ていただくと、足が接地したときに少しヒザを曲げている のが分かると思いますが、コレのことです。

実際の所は、「力のフィードバック」をやっていないので、それっぽく動かしているだけです。（笑）

はじめにこんな形のモデルがどう動くかを考えました。



• 運動は平面内に限定する。
• 関節Ｂ、Ｄは９０度に固定
• 足先Ａ、Ｃには、地面との間に、適当な摩擦係数（静・動）がある
• 支点がＡからＣに切り替わる時に、一定の割合で運動エネルギーが失われる
• 質量はｍの部分にだけある
• 構造ＡＢ、ＢＤ、ＣＤは剛体である
• これから作るロボットの性質を考えて、空気の抵抗は考慮しない
  

足首にかかる力を評価するために考えたモデルの、一番簡単なものです。


垂直方向から、θ傾いた位置で質量ｍの重りを、ｊ１に取り付けたモーターにて、静止状態で 支えるとします。 重力加速度をｇとおき、重りにかかる力ｍｇを、構造ｌの方向の力ｆ１と、構造ｌと直角な方向 の力ｆ２に分けて考えると、ｆ２＝ｍｇ・ｓｉｎθになり、ｊ１で発生しなければならない トルクｔ１はｌ・ｆ２となります。

例として前に倒れる境目の位置（ｍがつま先の上）まで来た時の必要トルクを２Ｌ１ｖ５の 数値を使って簡単に計算してみます。各数値は概略で以下の物とします。
ｍ＝１．４５（ｋｇ）
ｌ＝０．２３（ｍ）
ｘ＝０．０５（ｍ）

θ＝asin(x/l)より約12.56度
t1=0.23*1.45*9.812*sin(12.56)
=0.7116(N・m)
=7.2kg・cm

と言うような感じの計算をし、足首の必要トルクの目安にしています。


こんな風にして計算した値が、モーターのカタログスペックを常に越えるような状態を 発生させると、サーボモーターが壊れるという仕組みです。

以下の様な利点があるので、足先が通る軌道内部での加速・減速パターン にｃｏｓ関数を使用しています。

• 始めと終わりに速度がゼロ
• 積分すると面積（距離）が１
• コンパイラに標準装備の関数
• ちょうど真ん中で加速度がゼロ（速度は最大）

  y = cos(PI * x) + 1
  0 <= x <= 1.0
  PI：円周率
  x軸：時間、ｙ軸：速度
  
  この様に　面積（移動距離）１、経過時間１　の関数を単位ベクトルのように考えて、 任意の距離を任意の時間で移動する点列を作っています。
  軌道が３次元曲線の場合も、同じ長さを持つ直線上に点列を作り、曲線上に並べてゆく 事によって対応できます。
  
  

• 「地面は水平」と仮定する。
• 足底面は常に地面と平行
• 胴体は常に水平
• 腰の高さは一定
• 直進時に足は正面を向き、両足は平行

モデル化の前提

• サーボモーターは、外力に応じて入力信号から決まる目標位置とは異なる位置で止まって いると考えます。また外力によりバネ／ダッシュポット系の様な振る舞いをすると考えます。
• 関節から関節までをつなぐフレームは剛体として取り扱います。

制御の周期

ＲＣサーボに関していえば、50Hz（20msec）程度で入力のパルスを与えるためこの周波数が おおよその上限となります。１制御周期の間に１２個のサーボ用の位置データをサーボ コントローラーに入力し、ジャイロ等のセンサーのデータを読み込みます。
２Ｌ１ｖ５の場合はサーボにパルスを出す１周期の時間に１２回、8bitのパラレル入出力 を行う事が出来ます。しかし、入出力の対象が以下の様になっていますので、サーボの １周期の間に全ての入出力が終わらないため、以下に示す制御の周期になります。

• サーボデータをこれから送ることを知らせるコマンド（１バイト）
• サーボの角度データ（１２バイト／１２個分）
• これからセンサーのデータを読む事を知らせるコマンド（１バイト）
• ジャイロのデータ（２バイト／２軸）
• ＡＤＸＬ２０２のデータ（２バイト／２軸）
• 足裏タッチセンサーのデータ（１バイト）
• 合計　１９バイト

• サーボにパルスを出す周波数は４７Ｈｚ

  制御の周波数＝１／４７＊１９／１２＝0.03369sec＝29.68Hz

姿勢の制御

• 上記条件によれば、歩行中は胴体部分に回転運動が生じない事となりますので、 もしも回転運動が生じたら、姿勢を制御する必要が生じたとみなし、傾いてゆく方向と反対方向に 足首を動かします。姿勢制御動作の用のオフセットデータは、足先軌道から逆運動学計算により 求めた制御波形とは別に計算し、双方を重ね合わせて出力します。 軌道データには補正を加えません。
  この制御方法は、止まっている時、ゆっくりと動いている時、 もしくは動きを止めようとしている時に比較的うまく働きます。

２Ｌ１ｖ３で試した歩行パターンの足先軌道を図示してみました。

	フェイズ１ 右の足に重心を移します。
	フェイズ２ 左の足をその場で持ち上げ、前に送ります。そして、下ろします。 ロボットの重心を、足首関節中心の真上に保持出来れば、足首に力はかからない 訳ですが、遊脚だけを動かすと、ロボット全体としての重心が変わりますので、 重心は支持点の周りを移動します。また、足先の到達可能範囲が十分でないため 支持点直上まで重心を持っていけない場合も、足首で支えることになります。 この期間に、足型図形の中に重心があれば 転倒しませんが、足首のモーターが十分なトルクを発生できない場合は、支持点 から重心がずれるにつれて、だんだんとロボットが傾いてきます。 遊脚の移動速度をだんだんと上げて行きますと、反動が大きくなってゆき、 反動を打ち消すような動作（例えば手を振る等）を行わない限り立って いられなくなります。
	フェイズ３ 左の足に重心を移します。
	フェイズ４ 右の足をその場で持ち上げ、前に送ります。そして、下ろします。