計算を行うときに使用する座標軸と、各点に割り当てる記号を示します。ロボットを真上
から見た時の前後方向をX軸、左右方向をY軸、上下方向をZ軸とします。座標の原点は、
0番サーボの軸です。
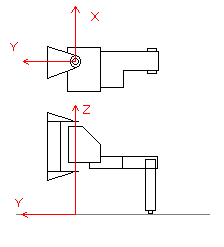
図1:座標軸の定義
次に脚の関節や、リンクの支点にAからFの記号を付けます。
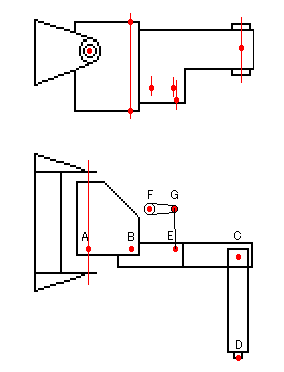
図2:支点の記号
脚の先端の座標から、その時の各関節の角度を求める様な計算を逆運動学計算といいます。
このページでは、6L1と4L1に使用した「脚」を例として、脚先端座標(x,y,z)から
各関節の角度(q0,q1,q2)を求める、計算手順につき説明します。
本サイトの2足歩行ロボット「2L1」でも、計算の拘束条件以外は似たような考え方で 計算を行っています。
計算を行うときに使用する座標軸と、各点に割り当てる記号を示します。ロボットを真上
から見た時の前後方向をX軸、左右方向をY軸、上下方向をZ軸とします。座標の原点は、
0番サーボの軸です。

図1:座標軸の定義
次に脚の関節や、リンクの支点にAからFの記号を付けます。

図2:支点の記号
ロボットを上から見た状態で点Aから点Dに線を引きます。ここで線分ADとY軸の交わる
角度を求めるとサーボ0の角度q0となります。
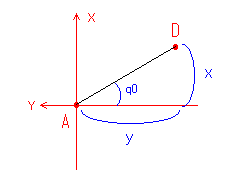
図3:サーボ0の角度計算
C言語で計算する場合はアークタンジェントの関数でatan2(x, y)とするとq0が求まります。
ここからはZ軸と点Dを含む平面で計算を進めます。これを作業平面と名付けます。
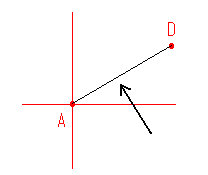
図4:作業平面の定義
新しく定義した作業平面では、数学の教科書などで見慣れているX軸、Y軸の方向で考えます。
ここでは点A,B,Dの座標が既知でCの座標が未知です。Cの座標を求めると関節BとCの
角度が求まります。
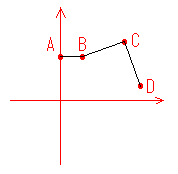
図5:作業平面
点Cは中心が点Bで半径が線分BCの長さの円、および中心が点Dで半径が線分CDの長さの
円との交点の1つとして求められます。2次方程式の解を求めると2つ求まりますので、常に
Y座標が大きい方の解を点Cの位置として使用します。
もしも交点が求まらなかった場合(2次方程式の解が虚数の場合)は、足先が届かない点が
指定されたということになります。よってプログラムはここまででエラーコードを返して
中断となります。
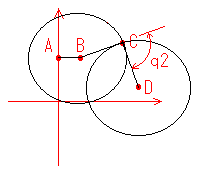
図6:点C
ここで線分BCと線分CDのなす角度を求めるとサーボ2の角度q2になります。
参考:2円の交点の求め方について、「数学1」の「図形と方程式」という辺りに
似たような問題が載っていました。
ここまでで点Cの座標が求まっていますので、X軸と線分BCのなす角度q3が既知です。脚が
中立位置にある時の点Eを点Bを中心としてq3回転させると現在の点Eの座標となります。
参考
高校の参考書では「代数・幾何」の「一次変換」に回転変換の説明がありました。
また、大学の教養の教科書では「線形代数」の範囲にありました。
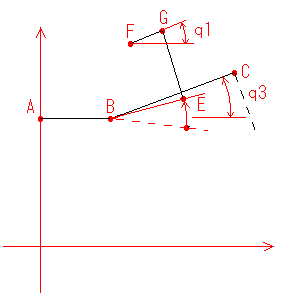
図7:点EとG
ここでは、点Eおよび点Fの位置、線分EG及び線分FGの長さが既知ですので、先に点Cの
位置を求めた時と同じ様に2円の交点を求める手法で、点Gの位置と線分FGの方向が求まります。
線分FGの方向がサーボ1の角度q1となります。
以上の手順で求めたq0,q1,q2をサーボに出力する8bitの数値に変換し、出力すると足先が希望の座標に動きます。
ここまでの説明でお気づきの方もいらっしゃると思いますが、この計算手順は脚のデザインによって
影響を受けます。サーボと関節の配置に仕方により、手順の長さ(計算の重さ)が変わりますので
ロボットを設計するときには、姿勢制御のサブルーチンがどの程度の重さになるかも予め考えに入れ
て設計すると良いでしょう。
参考書:
”逆運動学”について、一般的な議論が必要なければ、ここで説明した様に、高校までに習う
数学の知識で簡単に済ませてしまうことが出来ますが、本格的にいきたい方は
”ロボット工学”や”ロボットアームの制御” 等の題の付いた本に、一般的な計算方法が
説明されていますので、そちらを参考にすると良いでしょう。